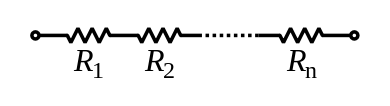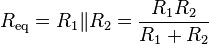Series and parallel resistors

Main article: Series and parallel circuits

In a series configuration, the current through all of the resistors is the same, but the voltage across each resistor will be in proportion to its resistance. The potential difference (voltage) seen across the network is the sum of those voltages, thus the total resistance can be found as the sum of those resistances:

As a special case, the resistance of N resistors connected in series, each of the same resistance R, is given by NR.
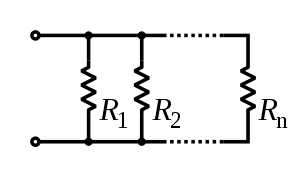
Resistors in a parallel configuration are each subject to the same potential difference (voltage), however the currents through them add. The conductances of the resistors then add to determine the conductance of the network. Thus the equivalent resistance (R_eq) of the network can be computed:

The parallel equivalent resistance can be represented in equations by two vertical lines "||" (as in geometry) as a simplified notation. For the case of two resistors in parallel, this can be calculated using:

As a special case, the resistance of N resistors connected in parallel, each of the same resistance R, is given by R/N.
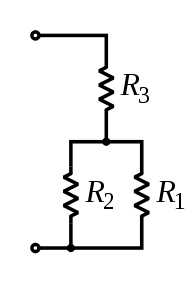
A resistor network that is a combination of parallel and series connections can be broken up into smaller parts that are either one or the other. For instance,

Ohm's law

The behavior of an ideal resistor is dictated by the relationship specified in Ohm's law:

Ohm's law states that the voltage (V) across a resistor is proportional to the current (I) passing through it, where the constant of proportionality is the resistance (R).
Equivalently, Ohm's law can be stated:

Color	1st band	2nd band	3rd band (multiplier)	4th band (tolerance)	Temp. Coefficient
Black	0	0	×100
Brown	1	1	×101	±1% (F)	100 ppm
Red	2	2	×102	±2% (G)	50 ppm
Orange	3	3	×103		15 ppm
Yellow	4	4	×104		25 ppm
Green	5	5	×105	±0.5% (D)
Blue	6	6	×106	±0.25% (C)
Violet	7	7	×107	±0.1% (B)
Gray	8	8	×108	±0.05% (A)
White	9	9	×109
Gold			×10−1	±5% (J)
Silver			×10−2	±10% (K)
None				±20% (M)